Expressões Regulares e Gramáticas

 Expressões Regulares (introdução)

Linguagem aceita pelos autômatos finitos.

 Concatenação

Se x é uma cadeia, então x* = {l , x, xx, xxx, ...} é um fechamento transitivo de concatenação.

Exemplos:

1-

(01)* = {l , 01, 0101, 010101, ...}

2-

abc*d = {abd, abcd, abccd, abcccd, ...}

3-

0*1* = {l , 0, 1, 01, 001, 011, 0011, ...}

4-

(0*1*)*1 = 0*1*0*1*...0*1*1

5-

(b*ab*a)*b* = cadeias de a's e b's com número par de a's.

 Expressões Regulares (definição)

Um símbolo qualquer é uma expressão regular.

Se x e y são expressões regulares, a sua concatenação xy também é uma expressão regular.

Se x é uma expressão regular, x* também é uma expressão regular.

A união de duas expressões regulares é uma expressão regular.

A expressão obtida por uma quantidade finita de aplicações da expressão regular a à expressão regular b é uma expressão regular.

Gramáticas

As gramáticas são produzidas pelo comportamento de autômatos finitos, como mostrado a seguir:

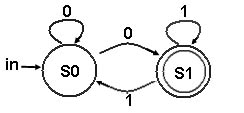
Produção:

S₀ ® 1 S₁ g(S₀,1) = S₁

S₀ ® 0 S₀ g(S₀,0) = S₀

S₁ ® 0 S₀ g(S₁,1) = S₀

S₁ ® 1 S₁ g(S₁,1) = S₁

Estados

Representação de estados INICIAL (S₀), FINAL (S₁ ® l )

Exemplo : Pelo autômato finito da figura anterior...

S₀ ® 0 S₀ | 1 S₁ P(1)

S₀ ® 1 S₁ | 0 S₀ | l

Dado o autômato finito abaixo:

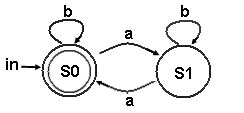
S₀ ® b S₀ | a S₁ | l P(2)

S₁ ® b S₁ | a S₀

Pode-se dizer que um autômato finito representa um reconhecedor e gramáticas representam geradores de cadeias.

Produções

S₀ Ü 0S₀ Ü 00S₀ Ü 001S₁ Ü 0010S₀ Ü 00101S₁ Ü 001011S₁ Ü 001011

Autômatos Finito como Gerador de Cadeias e Conjunto de Produções como Reconhecedor de Cadeias

ê

Zero ou mais passos de gerações

S_{0 ê}

0S₀

S_{0 ê}

00S₀

S_{0 ê}

001011

S_{0 ê}

00101S₁

Gramática (introdução)

Conjunto de regras de substituição de cadeias (produções)

Símbolo inicial

Símbolos auxiliares ou NT

Símbolos das cadeias finais geradas (T)

Gramática (definição)

Seja G uma gramática definida como G = (V_N, V_T, S, P); então

V_N : Alfabeto (conjunto finito) de símbolos NT

V_T : Alfabeto de símbolos T

S Î V_N

P : Conjunto finito de produções da forma a ® b

a Î (V_N U V_T)* - {l }

b Î (V_{N È} V_T)*

Exemplo 1:

X = {a, b}

X* = {l , a, b, aa, ab, ba, ...}

G₁ = ({S₀, S₁},{1, 0 , l }, S₁, { S₀ ® 0S₀ , S₀ ® 1S₁ , S₁ ® l , S₁ ® 0S₀ , S₁ ® 1S₁})

Exemplo 2:

G₂ = (V_N, V_T, S₀, P₂)

V_N = { S₀ , S₁} ; V_T = { a , b, l }

P₂ = { S₀ ® bS₀ , S₀ ® aS₁ , S₀ ® l , S₁ ® aS₀ , S₁ ® bS₁ }

Geração de Cadeias a partir de Gramáticas

Obs.: A seta preenchida (Ü ) está sendo usada para representar uma seta com uma bola preenchida em cima.

Exemplo: 001S_{1 Ü} 0010S₀

a = 001 ; b = l ; g = S₁ ; d = 0S₀

Definição: Dada uma gramática G = (V_N, V_T, S, P), dizemos que uma cadeia a gera uma cadeia b se existir uma seqüência de gerações diretas para G, da forma: a = a ₁ Ü a ₂ Ü ... Ü a _n = b , n ³ 1. Notação: a ê b

Obs.: A seta não preenchida (ê ) está sendo usada para representa uma seta com um asterisco em cima.

Exemplo: Considerando P₁ temos 001S_{1 ê} 001011S₁

Definição: Dizemos que uma cadeia a Î (V_N È V_T)* é uma forma sentencial de uma gramática G = (V_N, V_T, S, P) se S ê a .

Exemplo: Para P₁ temos as formas sentenciais: S₀ , 0S₀ , 00S₀ , ... , 001011aS₁

L(G) = {v Î V_T* | S ê v }

L(G) = {1, 01, 11, 001, 011, 101, 111, 0001, ...}

Definição (Equivalência de gramáticas): Duas gramáticas são equivalentes se, e somente se, L(G') = L(G'').

Correspondência entre Autômatos Finitos e Gramáticas

Definição: Seja um autômato finito M = (E, e₀, F, A, g). Uma gramática G = (V_N, V_T, S, P) é correspondente ao autômato finito M se:

V_N = E

V_T = A È {l }

S = e₀

P é constituído da seguinte forma: Uma produção N ® tQ para cada transição g(N, t) = Q e N ® l para cada N Î F.

Gramáticas (não regulares) mais gerais

Definição: São gramáticas mais poderosas do que as gramáticas equivalentes a autômatos finitos.

Exemplo: Gramáticas com produções da forma: N ® QRt, tNR ® Q, etc. com N, Q, R Î V_N e t Î V_T

Gramáticas Regulares

Definição: São gramáticas mais restritas e mais próximas das formas de produção correspondentes às transições de autômatos finitos.

Definição: Uma gramática G = (V_N, V_T, S, P) diz-se regular (GR), ou do tipo 3, se as suas produções são da forma: N ® tM ou N ® t', onde N, M Î V_N e t, t' Î V_T e t ¹ l .

Exemplo: G₃ = (V_N, V_T, S, P), onde V_N = {S, M},V_T = {a, b, c} e

M® bS

ý

P₃

G₃ é regular, L(G₃) = {c, bc, abc, ababc, ... , ddc, ...}

Vamos mudar P₃ para P₃' de uma gramática G₃', tal que L(G₃) = L(G₃') e G₃' corresponde a um autômato finito.

M® bS , N ® l

ý

P₃'

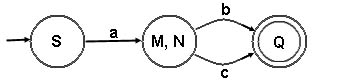
O autômato finito correspondente a G₃' é :

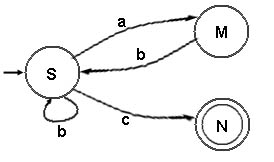
Teorema: Dada uma gramática regular G, existe um autômato finito M equivalente a ela, isto é, tal que L(G) é igual à linguagem aceita por M, e vice-versa.

Exemplo:

M® b , N ® c

ý

G₄'

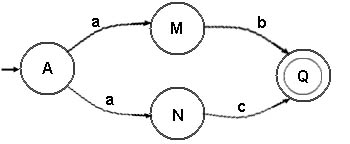
Autômato Finito não Determinístico

Introdução: g(S, a) = M , g(S, a) = N ; g é aplicação de transição.

Definição: Um autômato finito M = (E, e₀, F, A, g) é não determinístico se existirem e₁, e₂, e₃ Î E e a Î A tal que g(e₁, a) = e₂ e g(e₁, a) = e₃ , com e₂ ¹ e₃ ; caso contrário ele é determinístico.

Equivalência entre Autômatos Finitos Determinísticos e não Determinísticos

Equivalência entre Gramáticas Regulares e Expressões Regulares

Dada uma expressão regular E, existe uma gramática regular G equivalente, isto é, L(G) = E, e vice - versa.