Gramáticas e Árvores

 Gramáticas Livres de Contexto e Árvores Sintáticas

Definição: Uma gramática G = (V_N, V_T, S, P) é livre de contexto se as produções P estão são da forma N ® a , onde a Î (V_N È V_T)* e N Î V_N .

Exemplo:

i) E ® T | E + T | E - T

ii) T ® F | T * F | T / F

iii) F ® i | F ** i

E - símbolo inicial , i) , ii) e iii) correspondem à gramática G₅.

L(G₅): Expressões aritméticas com a variável i.

E ê i - i * i + i ** i

 Árvore Sintática

Representa, passo a passo a geração de uma cadeia por uma gramática.

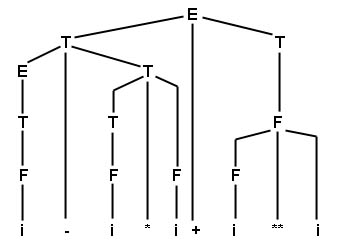
A árvore sintática fornece a estrutura gramatical da cadeia analisada.

E Ü E+ T Ü E - T+ T Ü T - T+ T Ü F - T+ T Ü i - T+ T Ü i -T * F + T Ü...

 Definição: Dada uma gramática livre de contexto :

1-

A árvore constituída inicialmente pelo nó rotulado S é uma árvore sintática.

2-

A árvore obtida pela substituição de uma folha (nó final), rotulada N, de uma árvore sintática, pela árvore

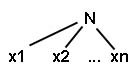
onde N ® x₁ , x₂ ... x_{n Î} P é uma árvore sintática.

Observações:

1-

A construção da árvore termina quando todas as folhas forem terminadas.

2-

A cada árvore sintática corresponde pelo menos uma geração.

3-

A cada geração corresponde pelo apenas uma única árvore sintática (embora várias gerações possam ter a mesma árvore sintática).

4-

Qualquer nó não folha é rotulado com um NT de G

5-

Um nó NT N e seus nós descendentes imediatos x₁ , x₂ ... x_n correspondem a uma geração direta N ® x₁ , x₂ ... x_n .

 Gramáticas Ambíguas

Definição: Dada uma gramática G = (V_N, V_T, S, P) ela é ambígua se existir uma cadeia x Î L(G) para o qual podem ser construídas duas árvores sintáticas diferentes.

Exemplo: E ® E + E | E * E | i (G₆)

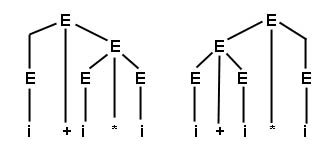
G₆ é ambígua.

Contra - exemplo:

S ® MN ; M ® a ; N ® b G₇

Uma única árvore sintática:

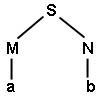
 Geração Canônica

Para que uma cadeia gerada por uma gramática corresponda a uma única geração, particulariza-se a geração da seguinte forma: Cada geração direta deve substituir o NT (não terminal) mais à direita.

Definição: Uma geração direta xNy ® xuy com N Î V_N e x, y Î (V_N È V_T)* é canônica se y contém apenas símbolos terminais.

Definição: Uma gramática G é ambígua se, e somente se, existir uma cadeia x Î L(G) para a qual exista mais do que uma geração canônica.

Exemplo: S ® S + S | i (G₈)

Portanto, G₈ é ambígua.

Seja a gramática G₇ : S ® MN ; M ® a ; N ® b

Esta gramática tem apenas uma geração canônica: S Ü MN Ü Nb Ü ab

 Comparação entre Gramáticas de Tipo 2 (Gramática Livre de Contexto) e Tipo 3 (Gramática Regular)

Toda gramática regular é uma gramática livre de contexto.

As produções das gramáticas regulares são mais simples do que as produções das gramáticas livres de contexto.

 Vantagens das Gramáticas Livres de Contexto sobre as Gramáticas Regulares

As gramáticas livres de contexto permitem a construção de árvores sintáticas mais complexas.

Chamamos a esta gramática de G₉ .

As árvores sintáticas correspondentes à cadeia i - i * i + i ** i serão:

Para a gramática G₅ :

Para a gramática G₉ :

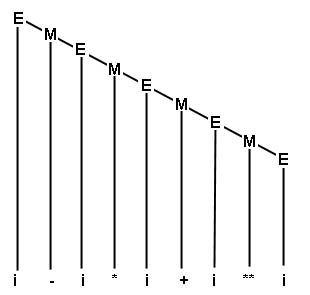
Todas as árvores sintáticas de gramáticas regulares são binárias. Cada nó tem:

1-

Um descendente terminal;

2-

Eventualmente, um descendente NT (não terminal);

A árvore sintática de gramáticas livres de contexto representam precedência entre as unidades sintáticas.

As gramáticas livres de contexto geram linguagens mais complexas.

1. E ® T | + T | - T | E + T | E - T
2. T ® F | T * F | T / F
3. F ® P | F ** P
4. P ® i | (E)

Chamamos a gramática descrita acima de G₁₀:

É impossível obter-se uma gramática regular que gere linguagens com sentenças balanceadas.

Exemplo: L = {aⁿ bⁿ | n ³ 1} é gerada por: S ® aSb | ab (chamaremos G₁₁)

 Autômato com Pilha

Assim como não existe uma gramática regular que gere sentenças balanceadas (ex.: L = {aⁿ bⁿ | n ³ 1}), não existe um autômato finito que a reconheça.

Para reconhecer linguagens geradas por gramáticas livres de contexto precisamos de autômatos com pilhas.

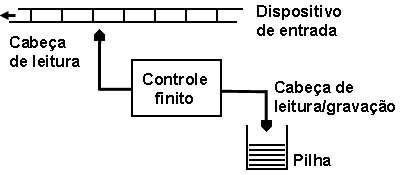
 Gramáticas Livres de Contexto com Expressões Regulares

Lado direito de cada produção com expressões regulares.

L(G₁₂) = a*b

NT definidos recursivamente

1-

N ® a *b

a , b Î (V_N È V_T)* ou são expressões regulares com símbolos de V_N e V_T

2-

N ® b *a