Introduction to Grammars and Language Analysis

Last Update Time-stamp: "97/06/30 13:49:02 umrigar"

Grammars

Any natural language like English or a programming language like Pascal has a vocabulary of words. For example, the vocabulary for Pascal contains words like for, x, ;, := or 1. A sentence of the language consists of some sequence of words taken from this vocabulary. For example, with the above vocabulary, we can compose the legal Pascal statement: 

	x:= 1
But not all possible sequences over a given vocabulary are legal, as the sequences need to meet certain syntactic and semantic restrictions. For example, with the Pascal vocabulary, we can construct the sequence of words 
	x:= for 1
which is syntactically illegal.

A context free grammar provides a method for specifying which of the sentences are syntactically legal and which are syntactically illegal. A context free grammar can be specified by a sequence of rules like the following (the rules are numbered for reference): 

1)	program:	stmts '.'
2)	stmts:		stmt ';' stmts
3)	stmts:		stmt
4)	stmt:		ID ':=' expr
5)	expr:		NUM
6)	expr:		expr '+' NUM
Each rule consists of a left-hand side (LHS) and a right-hand side (RHS) separated by a colon. The LHS contains a single symbol, whereas the RHS can consist of a (possibly empty) sequence of grammar symbols separated by spaces. Each rule can be viewed as a rewrite rule, specifying that whenever we have an occurrence of a LHS symbol, it can be rewritten to the RHS. For example, we can rewrite the LHS symbol program as follows: 
	program ==>	stmts .			by rule 1
                ==>	stmt .			by rule 3
		==>	ID := expr .		by rule 4
		==>	ID := NUM .		by rule 5
Note that the above rewrite sequence or derivation terminates as we cannot rewrite ID, :=, NUM or . any further because they do not appear on the LHS of any rule. Symbols like these terminate the derivation and are referred to as terminal symbols. The other grammar symbols which occur on the LHS of grammar rules are referred to as nonterminal symbols. The terminal symbols correspond to words in the vocabulary. The nonterminal symbols correspond to legal phrases or sentences formed using words from the vocabulary.

The terminal symbols are of two types: terminals which stand for a single word in the vocabulary and terminals which stand for a class of multiple vocabulary words. In the grammar, we denote terminals of the former type by enclosing the vocabulary word within quotes (for example, ':=' denotes the single vocabulary word :=), and denote symbols of the latter type with a name which uses only upper-case letters (for example, ID denotes the class of all vocabulary words which are identifiers).

Not all the phrases of a language are sentences in the language; for example, a Pascal statement by itself (a phrase) is not a legal Pascal program (a sentence). To ensure that a grammar describes only complete sentences, we distinguish one nonterminal called the start nonterminal from all others, and restrict all derivations to start from this distinguished start symbol.

We can now define a sentential form of a grammar G to be any sequence of grammar symbols (terminals or nonterminals) derived in 0 or more steps from the start symbol of G. A sentence is a sentential-form which contains only terminal symbols. The language defined by grammar G is the set of all sentences which can be derived from the start symbol of G.

To review, a context-free grammar G consists of a 4-tuple <N, T, R, S>, where N is a set of nonterminal symbols, T is a set of terminal symbols (disjoint from N), R is a set of rules, and S is a distinguished start nonterminal belonging to N. Each rule in R is of the form A: X, where A is a nonterminal in N and X is a possibly empty sequence of terminal and nonterminal symbols.

Note that a context-free grammar enforces only syntactic restrictions. It does not enforce any semantic restrictions on the sentences to ensure that they make sense. For example, a typical English grammar would allow the sentence

This page is swimming in the river
as grammatically correct, even though it does not make any sense.

Parse Trees

Consider a derivation of the sentence 
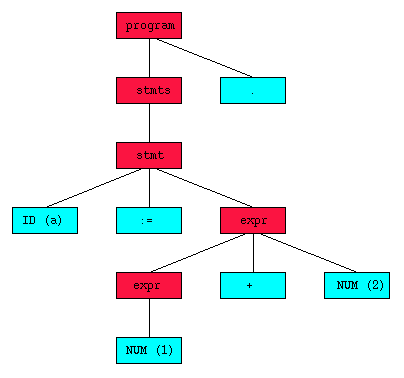
	a:= 1 + 2 .
in the above grammar (repeated here for reference): 
1)	program:	stmts .
2)	stmts:		stmt ; stmts
3)	stmts:		stmt
4)	stmt:		ID := expr
5)	expr:		NUM
6)	expr:		expr + NUM
The derivation proceed as follows: 
	program ==>	stmts .			by rule 1
                ==>	stmt .			by rule 3
		==>	ID := expr .		by rule 4
		==>	ID := expr + NUM .	by rule 6
		==>	ID := NUM + NUM         by rule 5
This derivation imposes a structure on the sentence which is shown by the following parse tree:
parse tree figure
The root of the parse tree corresponds to the start symbol. For each step in the derivation, when a LHS grammar nonterminal is replaced with the RHS of some grammar rule for that LHS, the RHS symbols are added as children to the node (shown in red) corresponding to the LHS symbol in the parse tree. After the derivation is complete, the leaves of the parse tree (shown in cyan) correspond to the terminal symbols in the sentence.

Language Analysis

We can analyze the sentences of a language by extracting the grammatical structure of the sentence. This is done by building an explicit or implicit parse tree for the sentence. The language analysis component of a system is usually organized as two distinct modules:
Scanner
The scanner accepts a stream of characters and breaks it up into words or tokens. A token gives the lexeme or actual text of the word as well as identifying what kind of word it is. The kind is usually encoded as a small integer. Hence the declaration for a token would look something like the following C typedef 
	typedef struct {
	  char *lexeme;		/* actual characters of token */
	  int kind;		/* class of token */
	} Token;
Parser
The parser accepts a stream of tokens from the scanner and extracts the grammatical structure of the sentence and builds (conceptually at least) a parse tree for the sentence.
language analysis block diagram

The parser can be organized so as to attempt to build a derivation of the sentence from the start symbol of the grammar. This kind of parser is referred to as a top-down parser, because in terms of the parse tree, it is built from the top to the bottom. Alternately, it can be organized so as to attempt to trace out a derivation in reverse, going from the sentence to the start symbol. This kind of parser is referred to as a bottom-up parser, because in terms of the parse tree, it is built from the bottom to the top.

A top-down parser needs to make two kinds of decisions at each step:

  1. It needs to choose a nonterminal in the frontier of the current parse tree to expand next.
  2. In general, a nonterminal may have several rules associated with it. Hence the parser needs to decide which rule to use to expand the nonterminal it chose in (1).
A bottom-up parser needs to make similar decisions.

A common organization used in batch compilers is for the parser to call the scanner whenever it is needs another token. Usually, the parser needs to look at one or more tokens to make its parsing decisions: these tokens which the parser is examining but not yet consumed are called lookahead tokens. Typically, the parser needs to use a single lookahead token.

Copyright (C) 1997 Zerksis D. Umrigar

Feedback: Please email any feedback to zdu@acm.org.

Up to Parsing Demos Main Page